0. はじめに
皆様お久しぶりです。初めての方ははじめまして。原田です。
弊社ももうすっかりScala会社になってきたなといった感じです。
Scala祭の将軍スポンサーやっておりますので、もしご興味があるかたはよろしくお願いいたします。
ScalaMatsuri 2016|日本最大級の Scala のカンファレンス
今回のネタはMonoidです。
簡単な実装例については、各所にありますがどういったところで使うと有用なのか?を模索するのにそこそこ時間かかったのでここにある一例を載せれればなと思っております。
1. Monoidってそもそも何なのよ?
初めて見た時よくわからなかったので補足をします。
1-1. S × S → S が与えられたとき
演算が集合に対し閉じている状態です。
これだけ言われても「ふぁっ?」ってなるのでもっと具体的に書くと
// 集合をHoge 演算子を|+|とした場合 Hoge型 |+| Hoge型 = Hoge型 //OK Hoge型 |+| Hoge型 = Fuga型 //NG //集合を整数 演算を+とした場合 Int + Int = Int //OK 演算が集合に対して閉じている状態! //集合をSeq[Int] 演算を++とした場合 Seq(1) ++ Seq(2) = Seq(1, 2) //OK 演算が集合に対して閉じている状態
1-2. 結合律
// 集合をHoge 集合の要素をa,b,c 演算を|+|とした場合 Hoge(a) |+| ( Hoge(b) |+| Hoge(c) ) = ( Hoge(a) |+| Hoge(b) ) |+| Hoge(c) // OKなケース // 集合を整数 演算を+とした場合 1 + (2 + 3) = (1 + 2) + 3 //OK 結合律を満たす // 集合をSeq[Int] 演算を++とした場合 Seq(1) ++ ( Seq(2) ++ Seq(3)) = (Seq(1) ++ Seq(2)) ++ Seq(3) //OK 結合律を満たす // NGなケース // 集合を整数 演算を - とした場合 1 - (2 - 3) != (1 - 2) -3 //NG 結合率を満たさない
1-3. 単位元の存在
// 集合をHoge 演算子を|+|とした場合 Hogeの単位元 |+| Hoge(a) = Hoge(a) |+| Hogeの単位元 = Hoge(a) // 上記に当てはまるような数値が単位元となります。 // 先ほどから上げている例で… // 集合を整数 演算を+とした場合 0 + 1 = 0 + 1 = 1 // 「0」が単位元 // 集合をSeq[Int] 演算を++とした場合 Seq.empty ++ Seq(1) = Seq(1) ++ Seq.empty = Seq(1) // 「Seq.empty」が単位元
2.実際にMonoid使ってすっきりしたケース
弊社アプリでは、次のようなレポートを排出しています。
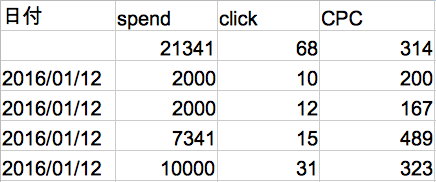
もうお分かりかと思いますが、お察しのとおり2行目のサマリー行を算出するところで、Monoidを使うと非常にすっきりしました。
2-1. 以前の実装
case class Row( spent:Long, click:Long ){
lazy val cpc = BigDecimal(spent) / BigDecimal(click)
}
// サンプルのため同一ファイルに定義してますが、実際は上位レイヤーのクラス
class ReportAggregateService {
def aggregate():Seq[Row] = {
val rows:Seq[Row] = ??? //サマリーを作る元となるデータを取得する
Seq(aggregateSummary(rows )) ++ rows
}
def aggregateSummary(rows:Seq[Row]):Row = Row(
spent = rows.map(_.spent).sum,
click = rows.map(_.click).sum
)
}
2-2.ScalazのMonoidで実装
import scalaz.Monoid
import scalaz.std.list._
import scalaz.syntax.foldable._
case class Row( spent:Long, click:Long ){
lazy val cpc = BigDecimal(spent) / BigDecimal(click)
}
object Row {
implicit val monoid: Monoid[Row] = new Monoid[Row] {
def zero: Row = Row(0, 0)
def append(f1: Row, f2: => Row): Row = Row(
spent = f1.spent + f2.spent,
click = f1.click + f2.click
)
}
}
// サンプルのため同一ファイルに定義してますが、実際は上位レイヤーのクラス
class ReportAggregateService {
def aggregate():Seq[Row] = {
val rows:Seq[Row] = ??? //サマリーを作る元となるデータを取得する
Seq(rows.toList.suml) ++ rows
}
}
3. まとめ
いかがだったでしょうか?
ReportAggregateServiceが非常にすっきりとした記載になっていることがお分かりいただけたでしょうか?
今回のサンプルコードでは指標を2つだけにしていますが、実際のコードでは10個以上の指標があり更にすっきりしています。
Monoidを使うとzero と appendを定義するだけでScalazのsuml等が使えるので非常に便利です。
2-1 のコードのケースですとaggregateSummaryに対して合算のテストが必要です。
今回のサンプルコードでは非常にシンプルな合計の形にしていますが、複雑なサマリー処理の場合にはテストケースも複数以上用意しなければならず億劫になります。
ところが、2-2のケースですと、zero と append 、および結合則のテストを行うだけでsumがいかに複雑であってもシンプルなテストになります。
Monoid怖くないよ!!
また、次の記事でお会いしましょうー。