数学が苦手な自分が機械学習の勉強で最初につまずいた確率について

こんにちは、株式会社FLINTERSの伊藤です。この記事は10周年記念として133日間ブログを書き続けるチャレンジの58日目の記事となります。

はじめに

私自身、数学が苦手で、特に確率については勉強を避けていて、センター試験では絶対選択していませんでした（笑）なので、機械学習で用いられる確率の勉強をはじめた時には基礎的な部分も分からず、つまずいてばかり。。。そんな確率も苦手な私ですが、試行錯誤してなんとか基礎は理解できるようになりました。私のような、数学苦手な人や、これから機械学習について勉強したい人に向けて、機械学習で使う確率の基礎について、なんとな〜く分かるを目標に説明していきます。

はじめに
確率
- 確率とは
確率変数
- 確率変数とは
離散と連続
- 離散とは
- 連続とは
確率分布と確率の関数
期待値
最後に

確率

確率とは

この部分は意外と、理解していなかったなと感じています。確率とはある試行を同じ条件で何度も何度も繰り返した時に、ある事象が起こる相対頻度の極限値です。 試行や事象、相対頻度や極限値など、よく分からない単語がありますよね。よく用いられるサイコロを例にとり、説明していきます。

試行：実際に行う行為のこと（サイコロを振る）
事象：試行をして観測された結果のこと（1の目が出る）
相対頻度：何かと比較した時の頻度のこと（サイコロを振った回数に対して1の目が出た回数を比較）
極限値：本来、答えは出ないが、限りなくある条件に近づけて行なった時に「この値に近づくだろう」といった値のこと

サイコロを振った時、1の目が出る確率は $\frac{1}{6}$ とされていますが、この値というのは、どのように求められるのでしょうか。例えば、試行の結果、以下のような相対頻度が出力されたとします（実際にサイコロを振ってみた時の値とは異なることがあるので注意してください）。

サイコロを10回振って、1目が3回出た時の相対頻度： $\frac{3}{10}=0.3$
サイコロを100回振って、1目が19回出た時の相対頻度： $\frac{19}{100}=0.19$
サイコロを1000回振って、1目が169回出た時の相対頻度： $\frac{169}{1000}=0.169$
サイコロを10000回振って、1目が1663回出た時の相対頻度： $\frac{1663}{10000}=0.1663$

このようにサイコロを何度も何度も振り続けます。 $\frac{1}{6}=0.16666...$ なので、試行を重ねるごとにだんだんと精度が良くなっていることがわかります。無限回サイコロを振った時には、 $\frac{1}{6}=0.16666...$ に近づくと思われます。つまり、サイコロの例で表した確率とは、ある試行（サイコロを振る）を同じ条件で何度も何度も（無限回）繰り返した時に、ある事象（1の目が出る）が起こる相対頻度の極限値（ $\frac{1666...}{10000...}=0.1666...= \frac{1}{6}$ ）のことです。

確率変数

確率変数とは

ここからが本題です。確率変数とは試行によりある値をとる変数のこと*1です。サイコロの例を用いると、サイコロを投げて出る目である $\lbrace1, 2, 3, 4, 5, 6\rbrace$ のことです。サイコロはどの確率変数 $(X)$ が出ても確率は $\frac{1}{6}$ であるため、式にすると以下のように表されます。

$\displaystyle P(X=x) = \frac{1}{6} \qquad X\in \lbrace1, 2, 3, 4, 5, 6\rbrace$

はい、私は初めこの式を理解できませんでした。え、「=」が2つあるけど何これ？ $P(X=x)$ ってなに？？？ひとつずつ分解して説明していきます。

$X$ ：確率変数のこと（サイコロの目が出る集合を $X$ と名付けていると捉えても構いません）
$X\in \lbrace1, 2, 3, 4, 5, 6\rbrace$ ：確率変数がとる値の範囲（サイコロの出る目 $X$ は $\lbrace1, 2, 3, 4, 5, 6\rbrace$ を含まれている）
$X=x$ ：確率変数が実際にとる値（サイコロの目が3の場合は $X=3$ と表す）
$P$ ：確率を算出する関数（確率変数 $X=x$ を確率を算出する関数 $P$ に入力）
$P(X=x) = \frac{1}{6}$ ：確率変数 $X=x$ を確率を算出する関数 $P$ に入力した結果 $\frac{1}{6}$ が出力される

このように確率を式で表すために確率変数は必要なんですよね。

離散と連続

離散とは

離散はデジタルとも言ったりしますが、流れ続ける現実の情報を区切って、飛び飛びに表したものをいいます。例えば、デジタル時計は連続する時の流れを数字で区切って表示しています。また、これまでの例で扱ってきたサイコロの目も離散的な値です。このように、ある特定の値しか取れないものを離散型、またそのような確率変数を離散型確率変数*2と言います。

連続とは

連続はアナログとも言ったりしますが、流れ続ける現実の情報をそのまま表したものを言います。例えば、アナログ時計は時間を示す針が連続して動き続けますが、決まった値を示すことができません。秒針が30秒付近を指していた場合、針の見た目は30秒っぽいが、正確な値は30秒ではなく、 30.00000001秒といった値を取ったりします。また、身長も同じく、170cmといった値は確率で存在しなく、170.00001cmだったり、170.0011cmだったりする値を切り捨てて170cmと表しています。このように、値と値の間に無限に取りうる値が存在するというのもが連続型、またそのような確率変数を連続型確率変数*3と言います。

確率分布と確率の関数

離散型と連続型にそれぞれ分けて確率分布と確率の関数を説明していきます。

確率分布とは

確率分布とは確率変数 $(X)$ に対して確率がどのように分布しているかを表したものです。この確率分布があるとデータの全体像が視覚的にわかるようになります。

離散型確率分布

離散型確率分布とは、確率変数が離散型である場合の確率分布のこと*4を言います。サイコロの例を用いて説明していきます。以下の表では、サイコロを振って出た目とそれに対応する確率を表でまとめたものです。

サイコロの目 $(X)$	$1$	$2$	$3$	$4$	$5$	$6$
確率 $P(X)$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$

この表でわかることは、サイコロを振って出た目（確率変数 $(X)$ ）に対応する確率はそれぞれ $\frac{1}{6}$ であるということ。この表を図で表すと以下のようになります。

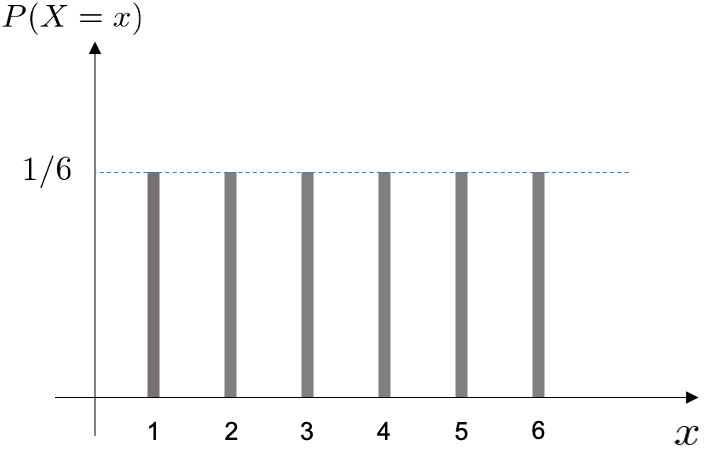
全ての確率変数において、同じ確率の値を取っていることが一目でわかりますね。このような確率分布は一様分布*5と言います。

確率質量関数

確率質量関数とは、確率変数が離散型である場合の確率を関数としたもの*6です。初めに「確率とは」でサイコロの例を用いた際に出てきた $P(X=x)$ が確率質量関数です。

連続型確率分布

連続型確率分布とは、確率変数が連続型である場合の確率分布のこと*7を言います。例えば、ランダムに1人選んだ成人男性の身長の連続確率分布は以下のように表されます（厳密には違う値かもしれませんが、ここでは例えの図です）。

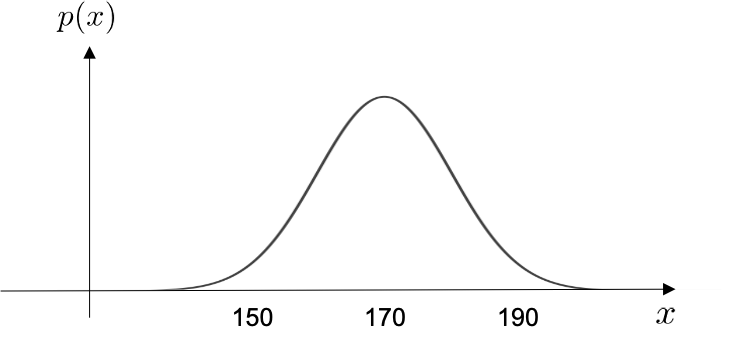
ポイントは、確率変数（横軸）の値が連続となっているため、離散型確率分布とは異なり、なめらかな一本の線で分布を描画できるということです。この分布を見ると、170cm付近の身長の方がランダムで抽出できる確率が高いことが視覚的にわかります。また、この分布の様に、1つの左右対称の山の形をした確率分布を正規分布*8と言います。

少し脱線してしまうのですが、この正規分布は本当に重要な理論で、世の中の社会現象や自然現象はこの正規分布に従っているものが多く存在します。気になる方は、正規分布と併せて、中心極限定理も調べてみてください。

確率密度

先ほどの離散型確率分布では縦軸に確率の値が表示されていて、イメージがわきやすかったと思いますが、連続型確率分布の縦軸は表示できておらず、一体縦軸は何なんだ？と思った方がいらっしゃるかもしれません。そうなんです、連続型確率分布の縦軸は確率密度なんです。もうよくわからないですよね？あれ、確率はどこいったの？？？私も本当にはじめは理解できませんでした。なるべくわかりやすくするために、噛み砕いて説明していきます。

連続型の場合の確率とは？

連続型の場合、確率分布の面積が確率となります。*9 度々用いているランダムに1人選んだ成人男性の身長について考えてみます。

身長が170cmちょうどである人の確率：「連続とは」で記述した通り、170cmといった値は存在しなく、厳密には170.00001cmだったり、170.0011cmだったりするので、170cmの人を抽出できる確率は0です。これを図で表すと以下の様になります。
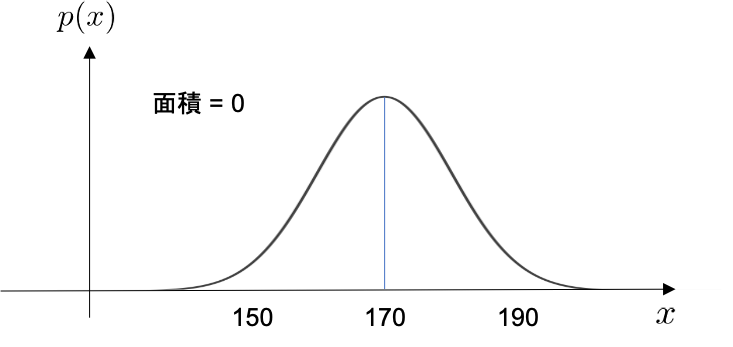
身長がちょうど170cmである人の確率

この図では線が見えてしまっていますが、この線の横幅は本来なく、0となります。面積を求めるとき、0をかけてしまったら、当然面積の値は0となります。

身長が150cmから170cmの間である人の確率：先ほどの例とは異なり、150cm~170cmと横幅を持たせています。これを図で表すと以下の様になります。
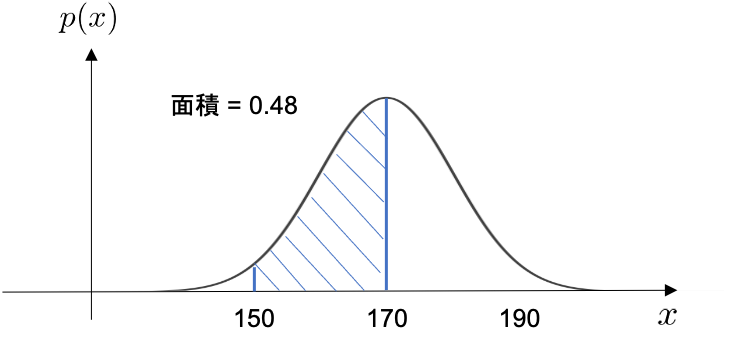
身長が150cmから170cmの間である人の確率

この様に、横幅があれば面積を求めることができます。つまり、確率も求めることができます。面積の求め方は積分を用います。（積分についての説明は省きます。すみません。とりあえず面積が求まるんだなくらいで大丈夫です。） 150cm~170cmの面積を求める式は以下の様になります。

$\displaystyle P(150\leq X\leq170) = \int_{150}^{170} p(x) dx = 0.48$

密度って何だっけ？確率密度とは？

厳密な言葉の意味は避けて、噛み砕いた説明をします。密度は何かしらに対する度合いです。よく聞く人口密度とは、人口に対して土地利用の度合いの目安となります。また、この度合いは何が便利かって、何かしらの値をかければ、何かしらの値が返ってきます。人口密度に面積をかけることで人口が求まります。確率密度も全く同じです。確率密度に横幅をかけると、確率が求まります。 確率密度があると150cm~170cmの人はかなりの確率で抽出できそうだな〜とわかるのです。つまり、確率密度とは確率を求めるためのものであり、確率変数に対しての「相対的な出やすさの指標」なのです。*10 冒頭で、「連続型確率分布の縦軸は確率密度」と説明しましたが、何となくお分かりいただけましたでしょうか。

確率密度関数

確率密度関数とは、確率変数が連続型である場合の確率密度を関数としたもの*11です。よく論文や海外の記事を見ると $PDF(Probability Density Function)$ と記されていることが多いです。

期待値

期待値とは、確率変数がとる値とその値をとる確率の積を全て足し合わせたもの*12です。離散型確率変数 $X = x_1, x_2, ..., x_i$ それに対応する確率 $P(X) = p_1, p_2, ..., p_i$ とした場合、以下のような式で表すことができます。

$\begin{eqnarray} E(X) &=& x_1 \times p_1 + x_2 \times p_2 + ... + x_i \times p_i \\ &=& \sum_{n}^{i=1}x_ip_i \end{eqnarray}$

これって何が役に立つの？と思いますよね。実は意外と身近なところで使われていたりします。宝くじを購入する際の意思決定の指標は、期待値によって定めることができます。 例えば、1本500円で引くことができる以下の様な宝くじ（全部で100本）があったとします。

当選金額 $(X)$	$10,000$ 円	$5,000$ 円	$1,000$ 円	$100$ 円	はずれ
確率 $P(X)$	$\frac{1}{100}$	$\frac{2}{100}$	$\frac{10}{100}$	$\frac{37}{100}$	$\frac{50}{100}$

この時の期待値を求めます。

$\begin{eqnarray} E &=& 10000 \times \frac{1}{100} + 5000 \times \frac{2}{100} + 1000 \times \frac{10}{100} + 100 \times \frac{37}{100} + 0 \times \frac{50}{100} \\ &=& 337 \end{eqnarray}$

この期待値から、1本宝くじを引くと平均で337円が出ることになります。言い換えれば、この宝くじを1本引くと平均で163円の損失があります。どうですか？この宝くじは引きたいですか？この様に、期待値を求めることで、宝くじを引くか引かないかの意思決定をすることができます（かっこよく言うと期待値原理と言ったりします）。実際にこのような確率変数はありませんが、期待値は確率変数の平均値のようなものです。続いて、連続型確率変数の場合は、以下の様な積分で表されます。

$\displaystyle E(X) = \int_{-\infty}^{\infty} x_ip_i(x_i) dx$

どこかで見たことがあるような式ですよね。そうです、連続型の確率の式と似ているのです。

ここで話はそれますが、期待値が生まれたのはギャンブルが背景となり、興味がある方もいらっしゃるのではないでしょうか。「メレの問題」や「パスカルの賭け」とかを調べてみると歴史的背景が見れるので面白いかもしれません。

最後に

確率は未来に起こる「可能性」を数値化したもので、簡単に行っちゃえば未来を評価できちゃうんですよね。なんだかかっこいいですよね（笑）また、情報理論と確率論の交わりは、AIブームのきっかけとなりました。ぜひ情報理論も併せて調べてみてください。（まずは「犬が人を噛む確率と人が犬を噛む確率」などと調べれもらえれば笑）

いかがでしたでしょうか。確率の基礎についてでした（本当は確率変数の変数変換までやりたかったけど、かなりのボリュームになってしまうため断念）。今回機械学習と絡めたことを全然記述できていなく、タイトル詐欺みたいになってすみません。けれど、機械学習を勉強するにあたって本当に重要な概念だと思っています！今回のブログでなとんとな〜く分かった気になれたり、少しでも興味が湧いてくれたら幸いです。

*1:統計WEB 『11-1. 確率変数と確率分布』

*2:AVILEN AI Trend 『離散型と連続型の違い例を用いて解説』

*3:AVILEN AI Trend 『離散型と連続型の違い例を用いて解説』

*4:統計WEB 『11-2. 離散型確率分布と確率質量関数』

*5:産総研『一様分布』

*6:統計WEB 『11-2. 離散型確率分布と確率質量関数』

*7:統計WEB 『11-3. 連続型確率分布』

*8:産総研『正規分布』

*9:統計WEB 『11-5. 連続型確率分布と確率1』

*10:統計WEB 『11-4. 確率密度と確率密度関数』

*11:統計WEB 『11-4. 確率密度と確率密度関数』

*12:統計WEB 『9-7. 期待値』